XHTMLBoy's Website

You are on a website dedicated to the enthusiasts of (valid) XHTML, and of beautiful mechanics.
Back to index

Some highlights of how this blog is generated

For several years (approximately 2), my friends Didier, Pierre and Xavier (that helped me so much in the writing of this article and designing diagrams, that he could easily be considered as co-author) worked on a very complicated library to do very complicated things: Preface. As mentioned in the README, the library is probably not very useful, but it allows you to develop in a rather funny style with lots of modules and weird names. After several months of development, as the only use of the library was in its unit tests. Xavier cordially asked me to experiment by building a concrete project with it. Although I didn't know OCaml, I assumed that it is the responsibility of a Java Champion to be versatile (so learn OCaml) but also to communicate (so have a blog). I started to create a static blog generator, which I modestly called "Wordpress" (the name has since been changed, for YOCaml, for obscure and debatable reasons). When the project started to be usable, it received input from several people to try to make it really usable. The content of the article differs slightly from the current implementation for pseudo-pedagogical reasons.

In this article, I will show you how a (future) Java Champion uses OCaml to test a library and build real software. It's possible that this article duplicates Xavier's presentation "Pratically unpractical Functional Programming for practical software". But don't worry, my aim is not to give the point of view of an obscure rigorous OCaml programmer, but to observe some implementation details under the eyes of a pragmatic developer, writing daily Go! and Java who decided... well, to learn OCaml. And since the pillars of YOCaml were described in a rather interactive Slack conversation, and I wasn't very inspired to write a new article, here's a selection of some tips and tricks used in the development of my static blog generator.

While one might question the practical viability of a static blog generator as a "real-world example", testing a library in a real-world context (however futile a static blog generator may be) can quickly cover usability or restriction issues. For example, several months after the merger of Freer monad into the main branch, a very cute ticket was raised (fortunately, a correction has been proposed). To avoid this kind of unforeseen problem, I decided to find a project that covered several of the less popular and generally less understood tools offered by Preface. Against all expectations... a static blog generator requires many of these tools and as a future Java Champion needs to communicate, I could ... kill two birds with one stone.

The general idea behind a static blog generator is quite easy, it is a special case of a build system. Great, the excellent paper "Build Systems à la Carte" provides a formal description (and implementation paths). Although Preface had all the necessary tools to respect the paper's implementation proposals... well... I was not aware of its existence when writing my implementation. That's a shame. Not being educated, I narrowed the scope of my experiment considering, somewhat naively, that a static blog generator is satisfied with :

Listing the actions that a generator must be able to perform, one quickly realizes that in fact... a static blog generator can very easily be implemented with make (and in addition sed and awk), but this would not really serve the cause of Preface! Anyway, here's an example of the typical flow you'd expect from a generator:

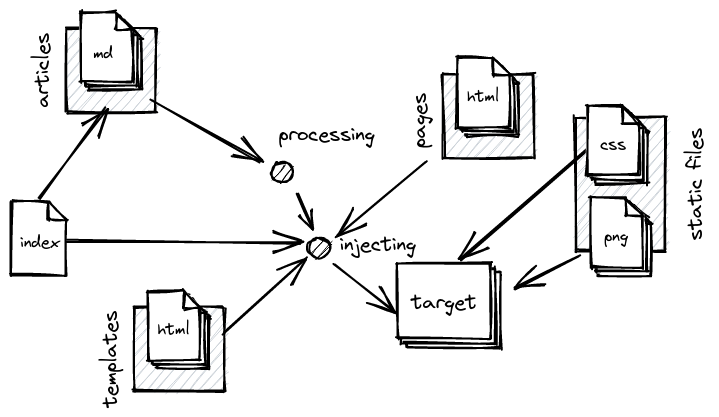
Here is a flow

Nothing very complicated, we move the static files (here, the CSS and the images) to the target. Then we inject the pages into the templates and move them to the target, then we process the articles (the markdown files) and inject them into the templates and move them, too, to the target. After all this, we can produce an index, which will probably be injected into a template and also moved to the target.

Now that we have the general flow of our generator, there are two considerations I would like to add. Firstly, I would like the generator to serve several use cases. It is therefore imperative that it not be restricted to a static file tree (imagine I wanted to create a cooking blog, listing recipes, I would find it morally unacceptable for the recipes to be in the articles directory). The second point concerns minimality. In other words, build only those artifacts that need to be built. (Since cryptocurrency miners use continuous integration service providers to mine bitcoin, saving computational time to generate during the continuous integration process is a must!)

The first point is fairly easy to address, just provide the generator as a library rather than as a binary. Backed by a rich API, a user (me) can build his generator with flexibility and not be locked into the rigid shackles of convention over configuration.

The second point is that we need to look a little more closely at the definition of minimality.

Minimality

Before diving into the code, it is important that we agree on the terms we will use. As mentioned earlier, by "minimality" I mean "the pressimistic reduction of the operations to be performed in order to construct an artifact". For example, let's imagine this scenario: we have 4 files needed to produce the a.out and b.out files. The first, a.md depends on A and the second, b.md depends on A and B. Let's see what happens if we change some files in the dependency graph. (In the example, a file that has been modified is drawn in red):

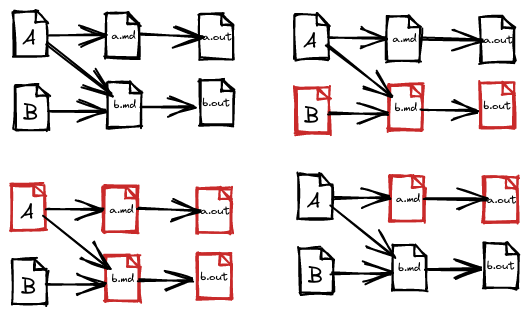
Minimality: scenario 2

Even if everything can be a little more complicated when dynamic dependencies are introduced (an element of the dependency graph which must be read to calculate ad hoc dependencies, but which will not be dealt with in this article, to avoid writing a 2000-page article), we would still like, in many cases, to reduce the calculation graph as much as possible when the dependencies are known statically.

Now that we agree on the terminology, we can go over some of the techniques used in the development of the blog generator!

About effect handling

When following the hype of the new generation of functional programming languages, one is often confronted with the problem of effects management. Yeah, effects are annoying because they often force the execution platform (imagine you want to run a generator in a browser), but effects are useful for making useful software.

There are monadic effects (or how to confine all troubles in a data of type IO a), there is algebraic effects adjoined to handlers, user-defined-effects (also adjoined to handlers, and generally to algebraic effects) or latent effects.

OCaml, prior to version 5, has a very peculiar (but very popular in the mainstream language world) effect system: god-given effects, which could be soberly renamed "side effects". Well, since OCaml handles effects on its own, why bother trying to process them "properly"? There are several ideological reasons which I will not detail, but essentially "to test the effects manager proposed by Preface". Let me introduce you to the Freer Monad!

Describing and interpreting with Freer monad

The difference between Free and Freer monad is quite subtle (and mainly based on differences in encodings and prerequisites), in use they offer similar capabilities. However, as Freer is significantly more efficient than Free, I have taken to using it exclusively. If you are familiar with Free, Freer is very accessible.

When writing programs that produce effects, a fairly standard technique is to separate the description of the program from its interpretation. The trick is to turn the execution of an effect into a value. We will only produce data structures, i.e. descriptions of programs, and we can provide them with an interpreter to concretely execute this program. Preface offers a fairly straightforward way to build descriptions and interpreters. We start by describing the operations that the program will be able to perform. For the example, I propose to reason about a program that can write or read (on the standard output) :

type _ operation =
  | Print : string -> unit operation
  | Read : string operation

And now we can build the combinators needed to describe programs by building a Freer monad for the operation type:

module Effect = Make.Freer_monad.Over (struct
  type 'a t = 'a operation
end)

The construction of tools for effects management produces, among other things, two very useful functions.

Using the first function (perform) we can easily describe a program, for example, let's just describe a program that displays "Hello World", asks the user to enter a value and displays "Hello" and the freshly entered value.

let print msg = Effect.perform (Print msg)
let read = Effect.perform Read

let program =
  let open Effect in
  let* () = print "Hello World" in
  let* name = read in
  print ("Hello " ^ name)

Note that the use of let* allows us to hide the fact that we are, in fact, manipulating a monad and allows us to describe our program in a style close to the direct style. Just use let* whenever you use a function described by the use of perform. The type of our program will be unit Effect.t and we now need to interpret it to give it an operational meaning. Let's write an interpreter for our set of effects:

let handler : type b. (b -> 'a) -> b Effect.f -> 'a =
 fun continue -> function
  | Print message ->
    print_endline message;
    continue ()
  | Read ->
    let line = read_line () in
    continue line

Interpreting an effect program isn't that complicated, you need to invoke a bit of ceremony to properly quantify the type variables (and yes, Freer uses an existential type, which makes inferring an interpreter impossible, hence why we should talk about iso-existential rather than existential), but once our type variables are properly quantified, a handler is nothing more than a pattern match on all the effects a program can produce, we execute the desired action and "continue" the program with what we just computed. At this stage, one can already quickly realise that it is possible to define an interpreter/handler according to the execution context. We could easily interpret our program in the context of the browser:

external console : unit -> hook Js.t = "caml_js_get_console"

let handler_js : type b. (b -> 'a) -> b Effect.f -> 'a =
 fun continue -> function
  | Print message ->
    (console ()) ## log (Js.string message)
    continue ()
  | Read ->
    let line = Dom_html.window ## prompt (Js.string "read") (Js.string "") in
    continue (Js.Opt.case (fun () -> "") Js.to_string line)

Yes, JS (especially in OCaml) is a bit verbose, but as you can see, you can change the execution context without touching the original program. One slight modification we could make to our interpreter for JavaScript would be to discard the continuation if the return of prompt is empty (not filled) but let's not dwell on the JavaScript.

Now that we have all the ingredients, we can actually run our program! And to do this, we'll simply use the run function defined in the Effect module:

let () = Effect.run { handler } program

This section was a quick overview of effects management with Preface, there is a more detailed guide in the Github repository which, if you are interested in the subject, I invite you to read and if you are really interested in the subject and you, unlike me, are able to read complicated papers, I invite you to read Free and Freer Monads: Putting Monads Back into Closet

Handler's composition

In the paper "Data Type à la Carte", a proposal of composition is given. Indeed, as in a Free monad, one builds a monad (for free) on top of a functor, it is enough to compose functors and to build a monad on top of the result of this composition. Although it is possible to propose a similar encoding for Freer (where the type on which the monad is built for free does not have to be a functor), I found it a bit verbose and boring... My proposal (which is also verbose and boring) is to centralise the definition of effects in a single type and to use a phantom type to allow only certain types to be indexed. But to have a flexible indexing (we would like to be able to selectively choose the effects we decide to interpret) we need to have a minimal support of row polymorphism. In OCaml, a restricted form of row polymorphism can be supported for sums by means of polymorphic variants and for products by means of objects. In YOCaml I used objects, but on reflection I find polymorphic variants easier to read. Let's change our operations to add an index:

type ('index, 'normal_form) operation =
  | Print : string -> ([> `Print ], unit) operation
  | Read : ([> `Read ], string) operation
  | Print_foo : ([> `Print_foo ], unit) operation
  | Print_bar : ([> `Print_bar ], unit) operation

Even though our operations have changed, we don't need to change much in our original handler so that it only supports Print and Read:

module Effect_A = Preface.Make.Freer_monad.Over (struct
  type 'a t = ([ `Print | `Read ], 'a) operation
end)

let handler_a : type b. (b -> 'a) -> b Effect_A.f -> 'a =
 fun continue -> function
  | Print message ->
    print_endline message;
    continue ()
  | Read ->
    let line = read_line () in
    continue line

Without going into detail, our handler which only supports the Print and Read effects is complete, and we can now create a module for the Print_foo and Print_bar operations and a handler:

module Effect_B = Make.Freer_monad.Over (struct
  type 'a t = ([ `Print_foo | `Print_bar ], 'a) operation
end)

let handler_b : type b. (b -> 'a) -> b Effect_B.f -> 'a =
 fun continue -> function
  | Print_foo ->
    print_endline "Foo";
    continue ()
  | Print_bar ->
    print_endline "bar";
    continue ()

And now that we have handlers for the different parts of the effects that we would like to be able to handle independently, we can create the module and the general handler, which handles the intersection of Effect_A and Effect_B by exploiting the handlers written earlier!

module Full = Make.Freer_monad.Over (struct
  type 'a t = ([ `Print | `Read | `Print_foo | `Print_bar ], 'a) operation
end)

let handler : type b. (b -> 'a) -> b Full.f -> 'a =
 fun continue -> function
  | Print _ as e -> handler_a continue e
  | Read -> handler_a continue Read
  | Print_foo -> handler_b continue Print_foo
  | Print_bar -> handler_b continue Print_bar

Some may say that we could have compacted the implementation of our handler composition... this is true but as each branch of the type has a different indexing and normal form, we would have had to be tricky and the final code would probably not have been readable.

So far so good, it is possible to compose handlers... is this useful in YOCaml... absolutely not. I just thought it was fun to experiment with another approach to effects handler composition which seems to be a restricted (but simpler) version of the Eff monad. OCaml making the expression of rows simpler (from my point of view) than Haskell.

Now that we have described all the stuff needed to manage effects (and that Preface offers, globally, sufficient tools), we will be able to look at the effects described in YOCaml to provide the tools needed to build static pages.

YOCaml effects

We've seen how to explicitly handle effects with Preface, and how, unnecessarily, to be able to compose different handlers, now let's see what effects we would want to propagate in a static blog generator. This is, in fact, a slightly more comprehensive list than the one mentioned in "What I want from a static blog generator", mentioned in the introduction to this article:

This list of requirements (which is a little longer in the YOCaml implementation to handle more specific cases) can be transposed quite easily into a list of operations (indexed or not. For code reading, and because for the purposes of this article, we won't need to handle only certain parts of the effects).

type 'a operation =
  | File_exists : filepath -> bool operation
  | Get_modification_time : filepath -> int Try.t operation
  | Read_file : filepath -> filecontent Try.t operation
  | Write_file : (filepath * filecontent) -> unit Try.t operation
  | Read_dir : (filepath * filepath predicate) -> filepath list operation
  | Log : string -> unit operation
  | Throw : Error.t -> 'a operation

There is not much subtlety (Try.t is a type that represents a valid value or an error, it is an Either whose error type is fixed). Note also that the Read_dir effect takes a predicate as an argument to prefilter the scanned children. We can move everything into a module (Effect for example), build our Freer monad and then implement the effect propagation combinators (so we don't have to keep using perform whenever we want to propagate an effect).

include Make.Freer_monad.Over (struct
  type 'a t = 'a operation
end)

let file_exists path = perform (File_exists path)
let get_mtime path = perform (Get_modification_time path)
let read_file path = perform (Read_file path)
let write_file path content = perform (Write_file (path, content))
let read_dir path predicate = perform (Read_dir (path, predicate))
let log message = perform (Log message)
let throw error = perform (Throw error)

An interesting point of this separation between the description of the program and its interpretation allows, for pedagogical reasons, not to worry about the interpreter at all. Rather than showing you soporific code that manipulates the file system, we can assume that our handler is correctly written, however, for reasons of logic, we will assume that the interpretation of the Throw effect will discard the execution of the continuation... and yes, if the code fails, we assume that we do not want to continue.. In addition, we can very easily build unit tests by providing a handler that, for example, hooks a file system into a mutable (or not) table. From now on, we can reason about the implementation of our blog generator without worrying about the concrete implementation of our functions. Great, isn't it?

One might ask why some effects return Try values when it is possible to fail with throw. This is essentially to force the fact that a function can fail into the handler. So we can add this convenience function to our Effect module:

 let failable eff =
    let* result = eff in
    match result with
    | Ok value -> return value
    | Error err -> throw err

It runs an effect that may fail, and, if it fails, catches its error and throws it with throw, otherwise it returns (wrapped in an effect) the result of the successful computation. I think this is a good way of enforcing in the handler that a function can fail but keeping it easy to use by not requiring the use of two levels of monads (Effect and Error).

This lengthy introduction has set out the requirements for starting to build a flexible library in earnest. The goal was to show that a Freer monad is simple enough to use and to lay the groundwork for building a true DSL for static page generation. Now we can look at the generation of pages while trying to ensure minimality.

Characterisation of a set of dependencies

Now that we have proudly described our primary operations... our effects, we can start looking at real problems! As mentioned in my expectations of a static blog generator, I want minimality! For example, let's say I want to build an out file which is the concatenation of a.html and b.html, i.e., in bash: cat a.html b.html > out, or, as this diagram visually describes:

Example of deps

It is easy to see that the file out has as dependencies a.html and b.html. We could imagine more complex scenarios. For example, imagine that the concatenation of a.html and b.html could be added to a c.html file to produce a new out2 file, as in this diagram:

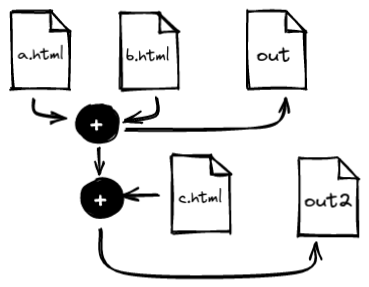
Example of complexe deps

In this much more complicated example, we can deduce that the dependencies of out are a.html, b.html and c.html. Elementary my dear reader. After this huge investigation (and with a little foresight), we can deduce some rules about how to represent our set of dependencies:

So, to recap, we are looking for "something" that can deal with the fact of not having dependencies (so has a neutral element), thus describing the absence of dependencies and that can be combined with other sets of dependencies (producing a new set of dependencies)... it is a monoid ! There was quite a clue in the chosen term "set of dependencies", the more seasoned private investigators will have noticed... a Set of dependencies is ... a Set of dependencies (e.g. of filepath, where string represents a path) and ... a Set is a monoid, elementary my dear, where the neutral element is the empty set and the internal law of composition (informally called "the oplus operator") is the set union.

Here is a proposal for the Deps module which will describe a set of dependencies and define some useful combinators. For now, we just export the fact that it is a monoid (in a Preface sense) and provide a function to convert a list of `filepaths' into a set of dependencies:

module Deps : sig
  type t

  val of_list : filepath list -> t
  val singleton : filepath -> t

  include Specs.MONOID with type t := t
end = struct
  module S = Set.Make (String)

  let of_list = S.of_list
  let singleton = S.singleton

  include Make.Monoid.Via_combine_and_neutral (struct
    type t = S.t

    let neutral = S.empty
    let combine = S.union
  end)
end

In this context, leaving the set of dependencies abstract allows, in the near future, to change the representation (if, by chance, I find a better representation one day). Now that we have a fairly naive definition of a set of dependencies, we can implement useful combinators!

Interweaving of dependencies and effects

Now that we have a robust representation of a set of dependencies (or, at best, an abstract, hence substitutable, representation), we can tackle the exploitation of our effects to answer a fundamental question in the generation of a static blog: "should an artifact be rebuilt or not?" To answer this very complicated question, we must first solve this very complicated equation system:

We know how to get the modification date of a file, just use Effect.(failable (get_mtime file)) but how do we handle a list (for dependencies)? In general, when you want to apply an operation on a list, you use map. The problem is that here, applying failable . get_mtime with map will give us a list of int Effect.t which is not very practical to use... Fortunately, when one does not know how to solve a problem in functional programming, there is a canonical answer: "it is traverse". And in this case, is sequence, which is a special case of traverse... so it is indeed traverse. In practical terms, Traversable allows us to switch from a list of effects to a list effect. First, let's define a traversable list of effects, and then a function which takes a list of filepath and returns an effect which contains the list of mtime:

module Traverse = List.Monad.Traversable (Effect)

let get_mtimes list =
  List.map Effect.(fun file -> failable (get_mtime file)) list
  |> Traverse.sequence

Great! We now have a function of type filepath list -> int list Effect.t and we can use it to implement the Deps.need_update function in accordance with the very complicated equation system mentioned above! As we have implemented all the requirements previously, the implementation of need_update is fairly trivial.

let need_update deps target =
  let open Effect in
  let* exists = file_exists target in
  if exists
  then
    let* target_time = failable (get_mtime target) in
    let+ deps_times = get_mtimes (S.elements deps) in
    List.exists (fun deps_time -> deps_time > target_time) deps_times
  else return true

Everything seems to be going well! We have all the plumbing for "doing things" by means of the Effect module and now we can describe sets of dependencies and check that an artifact is to be built (and ensure minimality). Now we need to build an API (or DSL) to provide the opportunity to build artifacts.

Definition of building rules

This part is strongly inspired, with the author's consent, by the presentation "Kotlin for functional programming? A brief introduction of Arrow" by Xavier, which briefly explains how YOCaml works (after an extraordinarily irrelevant introduction)..

The crux of the problem in a static site generator is ... generally, to write files that are the composition of several files. For example, let's imagine a minimalist blog, here is how we would like to create an article (without any consideration of effect management, think of it as pseudo-code):

let create_article file =
  let content = read_file file in
  Markdown.from_text content in
  |> inject_into "templates/article.tpl.html"
  |> inject_into "templates/layout.tpl.html"
  |> write_file ~into:"articles/" (change_extension file "html")

If we invoke create_article "my_first_post.md" we can make a first observation. The target is articles/my_first_post.html and the dependencies are my_first_post.md, templates/article.tpl.html and templates/layout.html. In the current form, it is not possible to do static analysis properly. However, the example captures an interesting insight, each step must describe dependencies. Let's start with the generator atom, reading a file.

To begin, we will define a type that will describe an action attached to dependencies. It is a kind of function, which produces an effect (and yes, we'll probably have to tinker with the file system) and which is attached to a set of dependencies.

type ('a, 'b) t =
  { deps : Deps.t
  ; task : 'a -> 'b Effect.t
  }

The advantage of this type is that it is easy to guess how to use it to create a file. Here is a proposal:

let create_file target { deps; task } =
  let open Effect in
  let* need_update = Deps.need_update deps target in
  if need_update
  then
    let* () = log "need to be created" in
    let* content = task () in
    failable (write_file target content)
  else log "nothing to do"

This function has the type filepath -> (unit, string) t -> unit Effect.t. Specifically, it takes a path (the file we want to create), and a value of the type we have previously defined and if the file is to be created, it writes it, otherwise it does nothing. Now that we can create files... let's implement a first action (a value of type ('a, 'b) t to read a file. reading a file generates only one dependency, the file to be read:

let read_file file =
  { deps = Deps.singleton file
  ; task = (fun () -> Effect.(failable (read_file file)))
  }

The type of read_file is filepath -> (unit, string) t. Perfect! This is just the type we need to test our create_file function!

let rule = create_file "my_page.html" (
  read_file "my_page.markdown"
)

Here, our variable rule has the type unit Effect.t, so in order to performs the file generation it is necessary to interpret it, exactly as we saw previously.

Effect.run { handler = my_handler } rule

We can read the contents of a file and write it elsewhere, but we would like to be able to apply a transformation to the contents of the file. For example, we would like to be able to transform the content of our file (which seems to be written in Markdown, given its extension) into HTML. As long as we have a function that transforms Markdown into HTML, writing the action that takes care of it seems quite trivial. As the action must act on content that has already been read, we know that the action will have no dependency, we can therefore use the neutral element of our monoid as a dependency.

let process_markdown =
  { deps = Deps.neutral
  ; task = (fun x -> Effect.return (Markdown.to_html x))
  }

Let's have fun seeing that we can, in fact, lift any unary function into an action! And yes, a function (which for example acts on strings) will have no dependencies (so it's just the neutral element of our monoid) and Effect.return allows to promote any regular value in a value wrapped in an effect! See how to refactor our action:

let lift f = {
  deps = Deps.neutral;
  task = (fun x -> Effect.return (f x))
}
let process_markdown = lift Markdown.to_html
let roaring = lift String.uppercase_ascii

As I have a lot of humor, I added roaring which allows to ROAR a text (transform its content into uppercase). But hey, okay, we can create actions, but don't you notice a little problem? How to connect read_file with process_markdown? Right now ... we can't really ... AHAHA.

Compose our actions together

You can proudly create actions but you can't connect them... that's sad! Let's see how to solve this very difficult problem. Let's proceed step by step! Composing the dependencies is pretty straightforward... and yes, I insisted like a moron that the dependencies form a monoid, so their composition is already present in their API: Deps.combine deps_a deps_b. Concerning the composition of the tasks, it is a bit more boring... what we would like is a function like this: ('b -> 'c Effect.t) -> ('a -> 'b Effect.t) -> 'a -> 'c Effect.t. We should be able to get away with something like this:

let compose a b =
  let open Effect in
  let deps = Deps.combine a.deps b.deps in
  let task x =
    let* f = b.task x in
    a.task f
  in
  { deps; task }

Ok, it works... but ... does the signature of the composition of the tasks remind you of something? Ahah excellent, indeed, the signature corresponds exactly to the composition of Kleisli! So rather than bother with complex considerations and unintuitive use of bind, let's use <=<!

let compose a b =
  let open Effect in
  let deps = Deps.combine a.deps b.deps in
  let task = a.task <=< b.task in
  { deps; task }

This is very cool, and what a coincidence, the Kleisli composition allows us to compose Kleisli arrows (yes, 'a -> 'b Effect.t is a Klesli arrow). Great, now we have a very unpleasant way to compose several actions!

let rule =
  create_file
    "my_page.html"
    (compose (read_file "my_page.markdown") process_markdown)

When you only compose two actions, the boring aspect of the function is not felt too much, but as soon as you decide to compose more actions... the pain is felt, like when you dip your lips in a too hot tea.

let rule =
  create_file
    "my_page.html"
    (compose
       (read_file "my_page.markdown")
       (compose
          process_markdown
          (compose
             roaring
             (compose
                roaring
                (compose roaring
                   (compose roaring
                      (compose roaring roaring)))))))

Yes, I know... I'm abusing, I'm shamefully taking advantage of the fact that the extraordinary roaring is idempotent to propose a not very credible example of what I call the compose-hell! and I'm a schemer at heart, so my tolerance to docked brackets should be battle tested! Fortunately, in the same way that JavaScript escaped from the Callback-hell using the then method, we'll be able to get away with defining ... an operator!

let ( >>> ) = compose

let rule =
  create_file
    "my_page.html"
    (read_file "my_page.markdown"
    >>> process_markdown
    >>> roaring
    >>> roaring
    >>> roaring
    >>> roaring)

The stairway to hell has been fixed with an operator and it is interesting to see that we are faced with a kind of composition of things that look like functions. However, not all our problems are solved. Indeed, as the function that produces the action to be executed is buried in a type, interacting with it is complicated. And so how to facilitate interactions between actions? Muehehe nothing easier, just add combinators and operators! Fortunately, there is an abstraction that captures the derivation of these combinators and operators!

Enter the Arrow

To simplify interactions with actions (our famous ('a, 'b) t type), it is necessary to construct complementary operators and combinators. Fortunately, much of the work has already been done in the previous section! As for monads (or applicatives), it is enough to implement minimal functions to derive a succession of useful combinators! In fact, our compose function, backed by an id value (of type ('a, 'a) t) is captured by an abstraction called Category and which provides all the composition operators. As we have already implemented compose, all that remains is to implement id, and its implementation is easy to guess. We want to use the two neutral elements of the two monoids that characterise an action (and yes, task is a monad which is ... a monoid in the category of endofunctors... what's the problem):

  module Category = Make.Category.Via_id_and_compose (struct
    type nonrec ('a, 'b) t = ('a, 'b) t

    let id = { deps = Deps.neutral; task = Effect.return }

    let compose a b =
      let deps = Deps.combine a.deps b.deps in
      let task = Effect.(a.task <=< b.task) in
      { deps; task }
  end)

We don't gain much compared to what we already had, it's just that we leave the generation of operators to Preface. The only concrete gain we have is the <<< operator, which is the reverse version of >>>. The only real point of describing Category is that it is needed to build Arrow, which builds on top of Category. There are several ways to describe Arrow but the one we are going to use requires, in addition to Category, an arrow function which is in fact exactly the lift function we implemented earlier and which lifts an arbitrary function into an arrow and a fst function. The fst function may seem a bit strange at first (and we'll describe it in more detail later), but its purpose is to transform a ('a, 'b) t value into ('a * 'c, 'b * 'c) t. It transforms the input of the function into a pair, applies the task to the first element of the pair and returns the application of the task coupled with the second element of the input pair which will not have changed. Although at first glance this function may seem completely useless, we will see that it is in fact very practical!

Here is an implementation of Arrow for our actions. In addition to building the Arrow module, I have included it in the rules module so that the combinators are present in the module's toplevel. I did not do this for Category as its combinators are included in Arrow:

module Arrow =
    Make.Arrow.Over_category_and_via_arrow_and_fst
      (Category)
      (struct
        type nonrec ('a, 'b) t = ('a, 'b) t

        let arrow f =
          { deps = Deps.neutral;
            task = (fun x -> Effect.return (f x)) }

        let fst a =
          let open Effect in
          { deps = a.deps
          ; task = (fun (x, y) -> let+ r = a.task x in  r, y)
          }
      end)

include (Arrow : Preface.Specs.ARROW
    with type ('a, 'b) t := ('a, 'b) t)

And... it was here that the Romans clashed... Arrow provides a plethora of combinators/operators. To understand their interest, I will try to explain them in as much detail as possible! Stay tuned.

Small note about Category, Strong profunctor and Arrow

An Arrow can be described somewhat pompously as a monoid (another one!) in the category of strong endoprofunctor. One could roughly rephrase this statement by saying that to have the full API of an Arrow, one would just have to add to a Strong Profunctor (present in Preface) a monoidal form. Here, Category. So there is no need to build Arrow, just provide Category and, on the same type, a Strong Profunctor. Moreover Preface provides a way to build an Arrow over Category and a Strong Profunctor. So why did we bother implementing Arrow which requires implementing more combinators (arrow and fst) when we can just implement dimap? This is a question I asked the Preface developers when they jointly added a hierarchy of arrows and profunctors. The answer can be divided into two distinct areas. Why in Haskell both hierarchies exist (and the answer itself breaks down into two distinct reasons) and why Preface (which is an OCaml library) seems to have consciously duplicated these closely related hierarchies.

In the case of Haskell, this is essentially because Haskell is a forerunner in the exploitation of abstraction from category theory. As a result, the hierarchy is not always fully stabilised. When arrows were introduced in Haskell in "Generalising Monads to Arrows" (in the context of parser combinators, what a surprise), the categorical correspondences of arrows were not yet fixed. It was not until many years later that the correspondence with strong profonctions was formalised (and very nicely summarised in the excellent "Notions of Computation as Monoids"). In addition, as for monads and applicative functors, arrows have a dedicated syntax: The Arrow Notation, explicitly implementing the different classes related to the arrows thus allows to benefit from a syntax "probably more pleasant to read". Hence the current interest in the concrete existence of the different arrow classes.

In the case of Preface, the very reasonable reason given was essentially that OCaml's lack of support (currently) for adhoc polymorphism means that in order to describe values of a type that is both a Strong Profunctor and a Category, there needs to be a functor (à la ML) that unifies Strong and Category, which needs to have a name... and Arrow seemed an appropriate choice.

The final question one might ask is why did I choose to implement Arrow rather than Strong (and then derive Arrow from Category and Strong)? Mainly because we had already implemented lift (which is arrow) and I found that implementing fst is more trivial than implementing dimap and that fst is, in use, more useful than dimap in the case of defining pipelines for generating static files.

After this little digression, let's have a look at some combinators to understand how to use them.

Arrow (and Category) functions

As mentioned earlier, our ('a, 'b) t type is a kind of function. However, since the function that corresponds to the action that needs to be performed is buried in a record, composing it and interacting with it is a bit complicated, plus we have to keep in mind to capture the dependencies intelligently every time. Fortunately, we have derived a set of utility functions so that we don't have to worry about these details, but since in the type ('a, 'b) t, a is in contravariant position and b is in covariant position, understanding the type signatures of the combinators derived by Arrow's generation can be tricky. So I propose to go through them one by one and understand their respective usefulness.

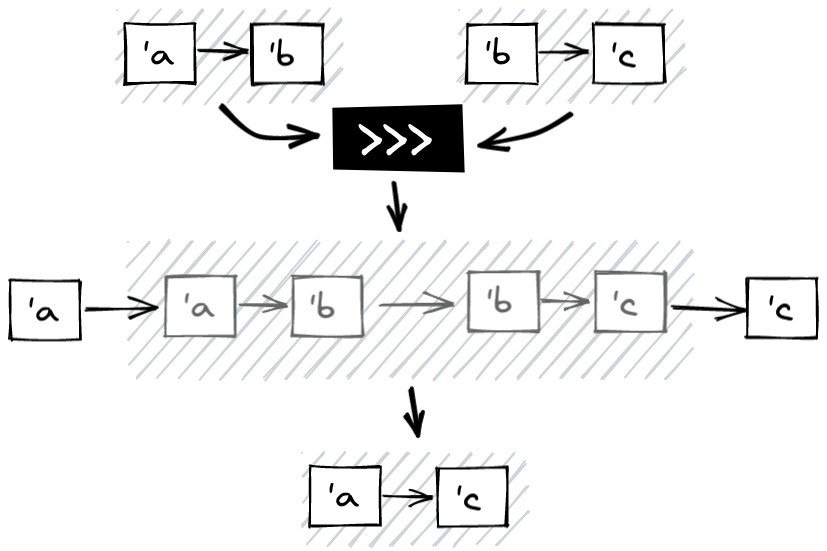
>>> (a.k.a compose)

We have already observed that >>> corresponds to the composition of Arrows. Suppose I have two arrows: f and g, of type ('a, 'b) t and ('b, 'c) t respectively, then f >>> g produces a new arrow of type ('a, 'c) t. This is function composition (from left to right) generalized to arrows. Concretely, the composition of arrow, in our context, will create a new arrow with as dependency, the union of f and g and the composition of kleisli of the task of f and the task of g.

arrow compose

If we reduced our arrows to functions, ignoring dependencies and effect, which is convenient because functions are also arrows (type ('a, 'b) t = ('a -> 'b)), >>> could be verbosely written in this way:

let (>>>) f g = fun x ->
   let y = f x in
   g y

The cool thing is that we had to code the operator by hand, to provide Category, and this is probably the most useful operator, it will allow sequencing each operation. To use the example in pseudocode we gave:

let create_article file =
  let content = read_file file in
  Markdown.from_text content in
  |> inject_into "templates/article.tpl.html"
  |> inject_into "templates/layout.tpl.html"
  |> write_file ~into:"articles/" (change_extension file "html")

Assuming that each operation (read_file, Markdown.from_text and inject_into) has an arrow, we don't need write_file because we had already defined the create_file function, it could be reformulated as follows:

val read_file : filepath -> (unit, string) t
val process_markdown : (string, string) t
val inject_into : filepath -> (string, string) t

let create_article file =
  let target = Filename.concat "articles" (change_extension file "html") in
  create_file target (
    read_file file
    >>> process_markdown
    >>> inject_into "templates/articles.tpl.html"
    >>> inject_into "templates/layout.tpl.html"
  )

We have seen that compose takes two arrows, and like any composition operator, there is its flipped version: f <<< g = g >>> f however, I have found fewer use cases, I find the order of execution unnatural.

The composition composes two arrows, but we have seen that arrow can promote a unary function to arrow, so there are combinators that shorten the composition of arrow with regular functions:

Which, assuming our Markdown.from_text function is a string -> string function, we could rewrite our previous example like this:

let create_article file =
  let target = Filename.concat "articles" (change_extension file "html") in
  create_file target (
    read_file file
    >>^ Markdown.from_text
    >>> inject_into "templates/articles.tpl.html"
    >>> inject_into "templates/layout.tpl.html"
  )

And as with all composition operations, there are flipped versions which we won't go into because I guess you get the idea. Keep in mind that the hardest part of this part has been done, >>> is really the core of the pipeline definition and the rest is just a bonus! Youhou.

fst, producing arrows with more than one parameter

Having seen how to sequence arrows, let's now look at the second of Arrow's prerequisites, fst. In the context of compose, we were constructing new arrows by sequencing. fst allows us to construct a new arrow that will wait for two parameters (in the form of a pair) and we return a pair where the first element is the application of the arrow on the first element of the pair and the second element of the pair is unchanged:

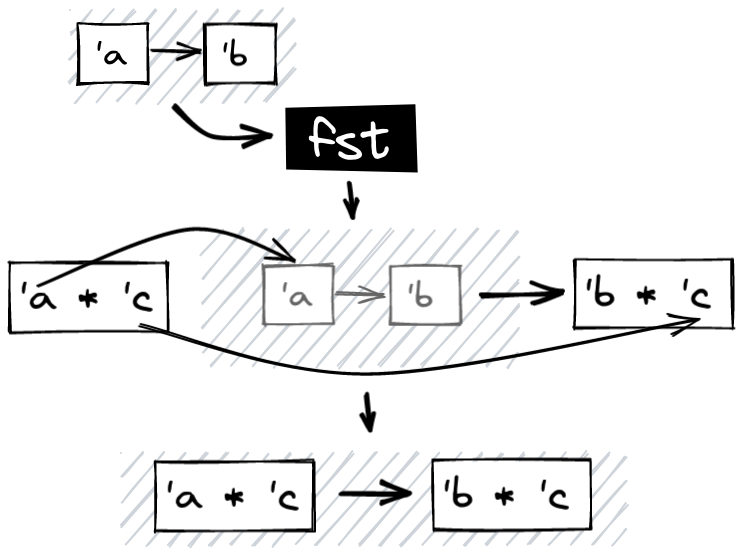
arrow fst

Just as with compose, let's abstract away the capture of dependencies and the effect to see what fst would look like in the context of functions:

let fst f = fun (a, b) ->
  (f a, b)

To understand its use, let's imagine we have a read_file_with_metadata function which assumes that when we read a file, we return a string * metadata option pair. It's quite common to attach metadata to a document, and we'd like to be able to read the document and its metadata, so what could be more relevant than to return a pair with the contents of the document and its potential metadata? However, the problem is that our markdown arrow will no longer be valid because at the reading stage, we no longer return a string, but a pair with a string and optional metadata. We would like to be able to process the markdown only on the first element of the pair. Aha, that's a good thing, we have a combinator to do just that! (We can also assume that inject_into takes a string and metadata pair (because the metadata is probably useful for building the layout) and returns a pair with the injected content and propagates the metadata.)

let create_article file =
  let target = Filename.concat "articles" (change_extension file "html") in
  create_file target (
    read_file_with_metadata file
    >>> fst process_markdown
    >>> inject_into "templates/articles.tpl.html"
    >>> inject_into "templates/layout.tpl.html"
    >>^ Stdlib.fst
  )

The last line of our arrow (>>^ Stdlib.fst) is necessary because the create_file function takes a target and an arrow of type (unit, string) t. So once we have processed our file, we can discard its metadata. Now that we have seen fst, it is very easy to guess what the next one will be... snd!

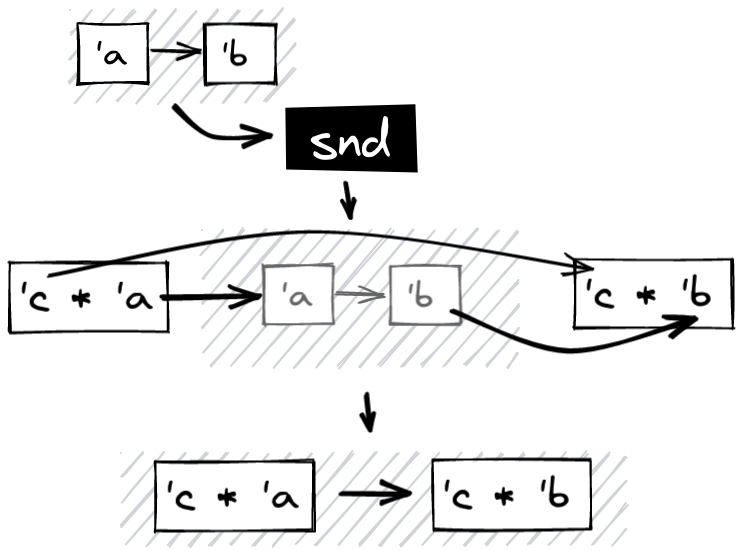
snd, producing arrows with more than one parameter (bis repetita)

No need to elaborate, snd is strictly analogous to fst, it just leaves the first parameter of the pair unchanged and applies the function to the second. In the same way as fst we go from an arrow waiting for an input to an arrow waiting for a pair.

arrow snd

As with fst, it is fairly easy to give the implementation in the function arrow (ignoring dependencies and effect) and the implementation, unsurprisingly, does not vary much from fst:

let snd f = fun (a, b) ->
  (a, f b)

At this point, one could imagine... a fst_of_three or third_of_fifty combinator (lol) but, in fact, fst and snd are enough. And yes, in the same way that a pair allows you to describe three pieces of data: (a, (b, c)) (yes, that's roughly how a list is described: type 'a list = (unit, 'a list) Either.t) you can describe three-parameter input arrows in this way: ('a * ('b * 'c), 'd) t. Which brings us to the major problem of the arrows! They imply an infamous way of programming and encourage the use of the horrible "point-free-style" (or Tacit programming... thanks APL, a great language that can sometimes tend to be unreadable, a bit like Perl in fact). Although Tacit programming can quickly give the impression that the person who wrote it is brilliant, let's face it, it can quickly become unreadable. Fortunately, in the generation of a static blog, one rarely needs anything that is not sequentially describable, which generally does not involve too much functional witchcraft.

But enough of this, let's take a quick look at two last operators, which can sometimes be useful.

*** (a.k.a split)

Thanks to fst we can produce, from an arrow that goes from a to b, a new arrow that goes from a pair of a and c and produces a pair of b and c, and thanks to snd we can produce, from an arrow that goes from a to b, a new arrow that goes from a pair of c and a and produces a pair of c and b, so from an arrow that goes from a to b and an arrow that goes from c to d, I could produce an arrow that goes from a pair of a and c to a pair that goes from b and d in this way: fst a >>> snd b. So here is split (***) which is a shortened form of the successive sequence of fst and snd:

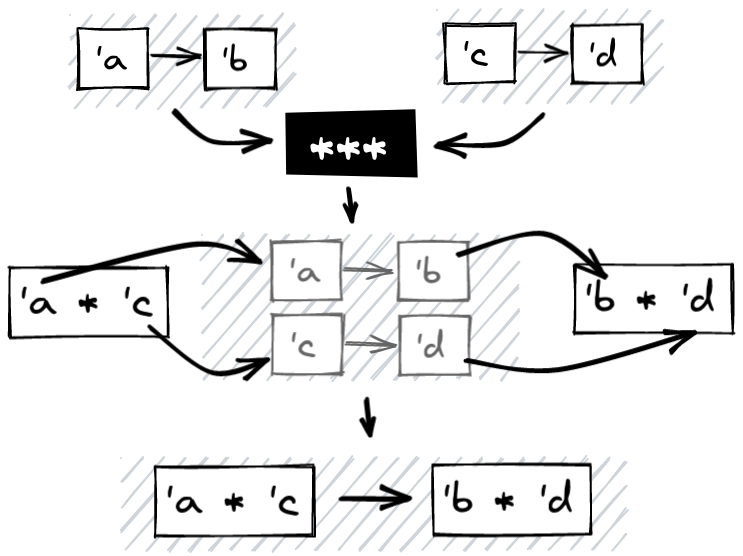
arrow split

And as with our previous operators, we can implement split for the arrow function, ignoring dependencies and effects, other than by using fst and snd (already given above):

let ( *** ) f g  = fun (a, b) ->
   (f a, g b)

And life is about equivalence, and we have seen that split can be expressed in terms of compose, fst and snd. Well, we can express fst and snd in terms of split!

let fst f = f *** id
let snd f = id *** f

Here the id is not the identity function but the id defined in Category, well... in the case of arrow functions... fun x -> x (i.e. the identity function) is the implementation of id (as Category).

Now that we have a way to reduce the complexity of our workflows by merging mergeable operations, thus avoiding the need to sequence successions of fst, compose and snd, we can turn our attention to the final combinator that I will introduce in this article!

&&& (a.k.a fan-out)

Our last operator allows us to apply two arrows to two elements. Another common operation that could be considered would be to apply two arrows to a single value. So for two arrows from a to b and from a to c, produce a new arrow that goes from a to a pair of b and c. Or apply two arrows to the same parameter simultaneously. Thinking only in terms of fst and snd we could imagine implementing this function like this: (fun x -> (x, x)) ^>> fst f >>> snd g. So here is fan-out (&&&) which is, like split a shortened of fst and snd.

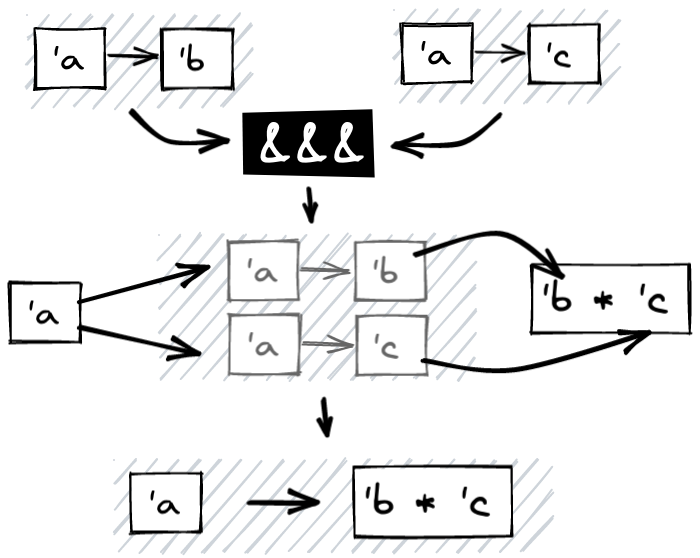
arrow fan-out

Without the ceremony of dependencies and effects, the arrow function that corresponds to this operation is, once again, quite easy to reason about:

let (&&&) f g = fun x ->
  (f x, g x)

Here are the operators and functions that can be used in regular arrows to build more complex arrows by assembly. Before drawing a conclusion of the exploitation of arrows, I would like to present you a small example of use.

Piping files using arrows

As I'm already up to my neck in shame, I'm stealing another example from Xavier (but which he took directly from the YOCaml code, so my honour is "a little bit safe")

The scenario is quite simple, we would like to be able to concatenate files, for example, to implement this case, or concatenate the files header.html, article.html and footer.html to build the file _build/article.html:

article.html: pages/%.html header.html footer.html
  cat header.html article.html footer.html > _build/article.html

Having already the arrow read_file (string -> (unit, string) t) there is a tempting approach to use &&, which we have just seen!

let concat_files file_a file_b =
  read_file file_a &&& read_file file_b
  >>^ (fun (content_a, content_b) -> content_a ^ content_b)

If the previous sections have been well understood, this code should not be a problem. read_file is a function which returns an arrow which expects unit as an argument, so we produce a global arrow which expects unit which we pass to the arrows produced by read_file file_a and read_file file_b, giving us a pair of the contents of file_a and file_b and then one promotes a regular function which simply concatenates two strings. If you are a hipster, you can rephrase this implementation as tacit (point-free for the win) and be hated by your coworkers (but by feeling smart, which is not to be overlooked):

open Preface

let concat_files file_a file_b =
  read_file file_a &&& read_file file_b
  >>^ Pair.uncurry ( ^ )

So far so good we now have a function of type filepath -> filepath -> (unit, filecontent) t. Cool, let's try to implement our example in Make:

concat_files "header.html" "article.html" &&& read_file "footer.html"
>>^ Pair.uncurry ( ^ )

Damn, what a mess! The type of our arrow gives us an indication that concat_files is not very exploitable: (unit, filecontent) t. What we would like is something like that:

read_file "header.html"
>>> pipe_content "article.html"
>>> pipe_content "footer.html"

Type of pipe_content is fairly easy to infer: filepath -> (filecontent, filecontent) t. As a starting point, we have the read_file arrow which starts from unit and returns a file content. So as pipe_content takes a file content and returns a file content, so we can focus on reading the file. As we saw earlier, we have a filecontent, and we would like a pair of filecontents, the second being the result of reading the file. We have a file content, unfortunately, read_file returns an arrow waiting for unit. One possible solution is:

arrow pipe

At this stage, we have our couple and we can just concatenate them!

let pipe_content filename =
  (fun x -> x, ())
  ^>> snd (read_file filename)
  >>^ (fun (content_a, content_b) -> content_a ^ content_b)

Unlike our first implementation, pipe_content is no longer restricted because its type is filename -> (filecontent, filecontent) t. The use of snd reinforces the idea that new arrows are being built.

Some closing words on our Arrow

After a first glance, one could quickly say that one of the most atrocious ways of programming has been highlighted! Replacing all function calls with Arrow pipelines is a very bad idea that forces tacit programming. How horrible! On the other hand, like the operators of Applicatives and monads (and many others), one can add context to a computation-sequence. Browsing through the various Arrows operators showed us the building blocks needed to construct sequential pipelines to which we added dependency capture and (almost transparent) effect propagation. And, not covered in this article, it is possible to capture other pervasive idioms in a language. For example, conditional jumps.

The main lesson about using arrows could be summarized into three doctoral assertions:

The usage of Arrow for a static blog generator is not new, it is even a rather obsolete way of doing it. Hakyll, prior to version 4, used dependency capture logic incredibly similar to that of YOCaml, funny! Hakyll decided to use a monadic construction to simplify the DSL. Since there is no real YOCaml-user, I will may be not facing this problem. Ahah. But it was all I want say about designing a DSL for creating generators. Joint with a good API, difficulties behind Arrows can be hidden. But it can be cool to understand what is under the hood. Let's move on the last big part of this too long article.

It is all about diversity

We have proudly designing, using Arrows, an almost-generic way to build generics (modulo the expressivity of our standard library) pipelines. We provide a kind of abstraction over effect handling (so also over the excution platform) and a kind of abstraction over sequential computation. But now, we will abstract over other things:

Abstracting over the markup language is not very complicated... it just a function from string (our filecontent) to filecontent Try.t (Try.t is a biased version of ('a, 'b) result, where all potentials errors are known). But abstracting over metadata and template engine is more complicated and pretty orthogonal. So here is a naive implementation (mainly written by Pierre) that is a almost smart usage of visitor pattern (as an aspirant Java Champion, I had to use almost one Design Pattern) , existential types, applicative validation and boilerplate. Let's imagine this flow:

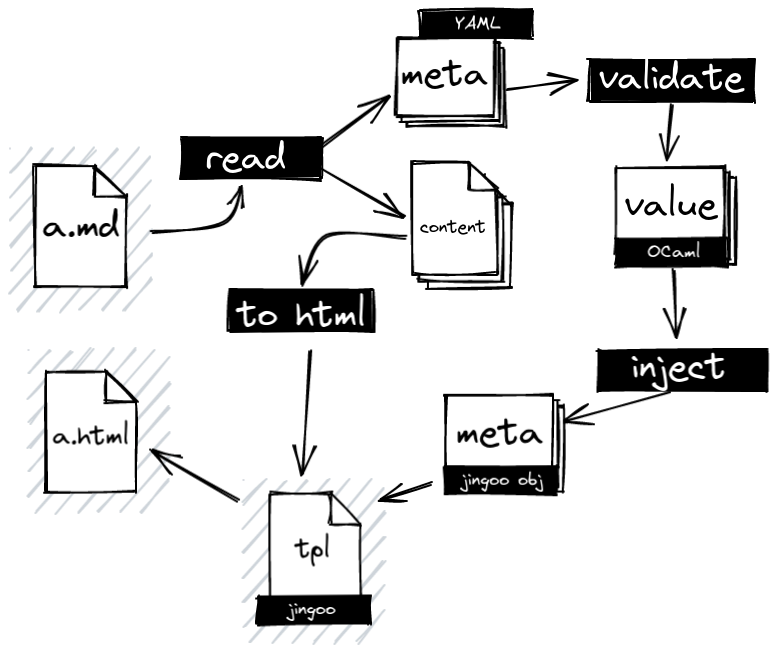
Tpl flow

Our a.md file looks like this:

---
title: I'm an article
date: 2021-11-12
author: The XHTMLBoy
---

Hello, **this is a first article in Markdown**.

I want, after reading, to have a pair of strings, the first element is the text between the --- and the second is the text after the second ---. For the content (the second element) I can just apply a function that transforms the markdown into HTML and it's done. But for the metadata (the first element of the pair) I have to do:

At this level, we quickly realise that the Markup language has little influence on the overall flow but that the template engine and metadata format impose anchor points for abstraction. (Hence the need for an intermediate type. One can only worry about having a function of MyMetaLanguage.t -> my_metadata and having my_metadata -> MyTemplateEngineMetaData.t to be able to connect the metadata to the template... through the magic of transitivity).

However, before going from our metaformat to our type which describes our metadata, we need to be able to transform a string into our format (for example Yaml). Ie: a module of this type:

module type READABLE = sig
  type t
  val from_string : string -> t Validate.t
end

Now we need to describe format-agnostic validators.

Metadata Validation à La Carte using Applicative functors and Visitor Pattern

The fact that we would like to use the Validation applicative is quite obvious, we want to collect all the errors in the metadata and not have to run the generator X times to catch X errors. So we know we'll be using Validation, which is fairly well documented in this guide. But if I decide to use TOML instead of YAML, I have to rewrite all of my metadata, ok, but it would be a shame if I had to rewrite my validation functions. No problemo, let's abstract over the notion of key-value! So far so good let's read the pattern bible again: Design Patterns: Elements of Reusable Object-Oriented Software.

Our goal is to describe what the components of a key-value representation are (which could, for example, at least represent JSON). And provide a fold function for each case. This gives us a rather naive version of the visitor! For YOCaml, we assumed that elements describing key-value structures could be integers, floats, booleans, strings, null values (because ... JSON), lists or objects.

type ('a, 'b, 'c) visitor = ('b -> 'c) -> (unit -> 'c) -> 'a -> 'c

module type VALIDABLE = sig
  type t

  val as_object : (t, (string * t) list, 'a) visitor
  val as_list : (t, t list, 'a) visitor
  val as_string : (t, string, 'a) visitor
  val as_boolean : (t, bool, 'a) visitor
  val as_integer : (t, int, 'a) visitor
  val as_float : (t, float, 'a) visitor
  val as_null : (t, unit, 'a) visitor
end

Our visitor type, ie: as_integer f g obj, can be read as: if obj is readable as an integer, extract the integer in x and apply f x, otherwise, apply g (). With the VALIDABLE interface you can generate validators. Here is the API of what I guess as sufficient for validating complex metadata. Firstly, simple validators are described. Visitors that simply wait for a value of the correct form.

type t

val object_ : t -> (string * t) list Validate.t
val list : t -> t list Validate.t
val string : t -> string Validate.t
val boolean : t -> bool Validate.t
val integer : t -> int Validate.t
val float : t -> float Validate.t
val text : t -> string Validate.t
val null : t -> unit Validate.t

Then, we can describe visitors that validate the correct form and then apply an additional validator (for example, to force a string to have a minimum number of characters, or to constrain the number of elements in a list):

val object_and : ((string * t) list -> 'a Validate.t) -> t -> 'a Validate.t
val list_and : (t list -> 'a Validate.t) -> t -> 'a Validate.t
val list_of : (t -> 'a Validate.t) -> t -> 'a list Validate.t
val string_and : (string -> 'a Validate.t) -> t -> 'a Validate.t
val boolean_and : (bool -> 'a Validate.t) -> t -> 'a Validate.t
val integer_and : (int -> 'a Validate.t) -> t -> 'a Validate.t
val float_and : (float -> 'a Validate.t) -> t -> 'a Validate.t
val null_and : (unit -> 'a Validate.t) -> t -> 'a Validate.t

Now we can deal with the objects, by processing their fields:

val optional_field
    :  ?case_sensitive:bool
    -> (t -> 'a Validate.t)
    -> string
    -> t
    -> 'a option Validate.t

  val optional_field_or
    :  ?case_sensitive:bool
    -> default:'a
    -> (t -> 'a Validate.t)
    -> string
    -> t
    -> 'a Validate.t

  val required_field
    :  ?case_sensitive:bool
    -> (t -> 'a Validate.t)
    -> string
    -> t
    -> 'a Validate.t

The interesting point is that, if we provide a VALIDABLE (i.e. the short list of visitors), we can describe the complex set of validations just listed. For example, here are some example implementations (the others are easy enough to guess):

module Make_validator (KV: VALIDABLE) = struct

  let string_and additional_validator =
    KV.as_string additional_validator (fun () ->
        Validate.error $ Error.Invalid_field "String expected")

  let string = string_and Validate.valid

  let optional_aux kind case_sensitive validator k s =
    Option.fold
      ~none:(Validate.valid None)
      ~some:(fun x -> null_and (fun () -> Validate.valid None) x <|> validator x)
      (find_assoc ~case_sensitive k s)

  let optional_field ?(case_sensitive = false) validator k s =
    object_ s
    >>= optional_aux
      "field" case_sensitive (map Option.some % validator) k

  let optional_field_or ?(case_sensitive = false) ~default validator k s =
    optional_field ~case_sensitive validator k s
    >|= Option.value ~default

  let required_field ?(case_sensitive = false) validator key subject =
    optional_field ~case_sensitive validator key subject
    >>= Option.fold
          ~none:Error.(to_validate (Missing_field key))
          ~some:Validate.valid
end

Yes, this code may seem complicated, but the big advantage is that it is totally hidden to the user! Let's say I want to build a validator for Yaml, here is the representation of Yaml in its OCaml library:

type value = [
| `Null
| `Bool of bool
| `Float of float
| `String of string
| `A of value list
| `O of (string * value) list
]

It is incredibly easy to describe a validator! Well, I grant you that it is a bit boring, but at least the lack of difficulty gives credit to the previous code!

module Yaml_validator = Make_validator (struct
  type t =
    [ `Null
    | `Bool of bool
    | `Float of float
    | `String of string
    | `A of t list
    | `O of (string * t) list
    ]

  let as_object valid invalid = function
    | `O kv -> valid kv
    | _ -> invalid ()

  let as_list valid invalid = function
    | `A v -> valid v
    | _ -> invalid ()

  let as_string valid invalid = function
    | `String s -> valid s
    | _ -> invalid ()

  (* etc. *)

  let as_null valid invalid = function
    | `Null -> valid ()
    | _ -> invalid ()
end)

We have proceeded in exactly the same way as in the previous sections. We describe some boring code "as a library producer" to make it easier for the user to use "the library as a consumer". To move on to the next step, we need a first ingredient: a function that separates the content of a document from its metadata: filecontent -> (string option * filecontent), this function is not very interesting but it will extract the bounded content in the --- and the content after the metadata description. The metadata is described as potentially absent (hence the option) because it is conceivable that a document has no metadata.

Now we can extend our READABLE module by saying that READABLE data is also validatable by injecting a VALIDATOR:

module type READABLE = sig
  type t
  include VALIDATOR with type t := t
  val from_string : string -> t Validate.t
end

The READABLE module is able to transform a string into our metaformat and provides a minimal validation API. Now we need to be able to actually define a validation scheme for data. We can add a new module which will project our metaformat into a metadata type using the READABLE combinators to provide validation:

module type PROJECTABLE = sig
  type t
  val from_string : (module READABLE) -> string option -> t Validate.t
end

The purpose of this from_string function is to start with our metadata option and use an READABLE module given as an argument to validate the data and concretise our metaformat into metadata. For example, let's implement the metadata of an article as shown in our example:

module Article = struct
  type t = {
    title: string
  ; date: Date.t
  ; author: string option
  }

  let make_metadata title date author =
    {title; date; author}

  let from_string (module R: READABLE) = function
    | None -> Validate.error (Error.Required_metadata [ "Article" ])
    | Some str ->
      R.from_string str >>= R.object_and (fun obj ->
        make_metadata
        <$> R.(required_field string) "title" obj
        <*> R.(required_field Date.validator) "date" obj
        <*> R.(optional_field string) "author" obj
end

If you are not familiar with applicative validation, I invite you to re-read the Preface guide. The good thing is that thanks to our visitor-derived validation, we can write validation schemes that don't care about the metaformat. For example, ensuring that a string is an email address, or that a list is non-empty. The use of Date.validator (the implementation of which is not given) indicates that we can correctly compose our validators. All for the best!

Now let's package everything in an arrow to facilitate the use of our reader/validator on demand:

let read_file_with_metadata
    (type a) (module R: READABLE) (module P: PROJECTABLE) filepath =
    read_file filepath
    >>^ split_metadata
    >>> fst (arrow (P.from_string (module R)))
    >>> (lift_task (function
          | Valid x -> Effect.return x
          | Invalid x -> Effect.throw (Error.of_list x)))

lift_task has type ('a -> 'b Effect.t) -> ('a, 'b) t. This is a bit like arrow except that the function returns an effect. The type of our read_file_with_metadata arrow is :

val read_file_with_metadata
  :  (module READABLE)
  -> (module PROJECTABLE with type t = 'a)
  -> filepath
  -> (unit, 'a * string) t

After running our arrow, we have a pair with our correctly parsed metadata as the first element and the content of our document unchanged as the second. The interesting thing about this approach is that it makes Article (the description of our metadata) completely format-agnostic. Everything is abstracted using the READABLE module. We could simplify our code by providing, in the modules that describe our metaformat, for example in Yocaml_yaml an arrow that avoids having to give two modules (we suppose that Readable is defined in Yocaml_yaml and contains the Yaml_validator we defined earlier and the function from_string, of course):

let read_file_with_metadata
    (type a) (module P : Yocaml.PROJECTABLE with type t = a) filepath
  = Yocaml.read_file_with_metadata (module Readable) (module P) path

Great, we have the generic projection (i.e. reading text data, and validating it) defined. Now to deal with the various template engines, we would need the generic injection, which is the transformation into a format interpretable by a template engine.

Metadata injection à La Carte, without any fancy trick

As most of the work has been done before, one must sadly note that the injection is super easy and does not rely on any complicated Java Champion techniques... We only have to provide the opposite of our visitors. Instead of "visiting cases", we provide combinators to produce cases.

module type DESCRIBABLE = sig
  type t

  val object_ : (string * t) list -> t
  val list : t list -> t
  val string : string -> t
  val boolean : bool -> t
  val integer : int -> t
  val float : float -> t
  val null : t
end

And, for example, for Yaml, you can provide a descriptor very simply by reusing the type of Yaml_validator:

module Yaml_descriptor = struct
  type t = Yaml_validator.t

  let object_ list = `O list
  let list list = `A list
  let string str = `String str
  let boolean b = `Bool b
  let integer i = `Float (float_of_int i)
  let float f = `Float f
  let null = `Null
end

Now, as we have described what readable metadata is. We need to describe what is injectable metadata. Nothing could be simpler! Instead of having from_string we need a inject function. That function will take a t describes it as a list of key attached to values DESCRIBABLE.

module type INJECTABLE = sig
  type t
  val inject :
    (module DESCRIBABLE with type t = 'a) -> t -> (string * 'a) list
end

We can easily improve our Article module to describe the metadata :

module Article = struct
  type t = {
    title: string
  ; date: Date.t
  ; author: string option
  }

  let make_metadata title date author =
    {title; date; author}

  let from_string (module R: READABLE) = function
    | None -> Validate.error (Error.Required_metadata [ "Article" ])
    | Some str ->
      R.from_string str >>= R.object_and (fun obj ->
        make_metadata
        <$> R.(required_field string) "title" obj
        <*> R.(required_field Date.validator) "date" obj
        <*> R.(optional_field string) "author" obj

  let inject
    (type a) (module D: DESCRIBABLE with type t = a) {title; date; author} =
    [ "title", D.string title
    ; "date", D.object_ (Date.inject (module D) date)
    ; "author", Option.fold ~none:D.null ~some:D.string author ]
end

By structural subtyping, which applies to modules, Article can be interpreted as a PROJECTABLE and a INJECTABLE! And as before, for READABLE, we would like to be able to project our injectable data into the format of our template engine, so we can add a RENDERABLE module whose purpose is to inject our data into a template engine:

module type RENDERABLE = sig
  type t
  include DESCRIBABLE with type t := t
  val to_string : (string * t) list -> filecontent -> filecontent
end

Let's package everything in an arrow!

let apply_as_template
  (type a) (module I: INJECTABLE) (module R: RENDERABLE) template_file =
  let action ((meta, content), tpl_content) =
    let data = I.inject (module R) meta in
    let variables = ("body", R.string content) :: values in
    R.to_string variables tpl_content
  (fun x -> x, ())
  ^>> snd (read_file template_file)
  >>^ action

The first observation is that we use the same trick as for piped_content to avoid locking up our arrow and make it composable (i.e. applying apply_as_template several times to get a hierarchy of templates. The second observation is that the content of the file is added as data to be injected into the template to allow the user to arbitrarily choose where to inject the content. The type of our apply_as_template arrow is :

val apply_as_template
  :  (INJECTABLE with type t = 'a)
  -> (RENDERABLE)
  -> filepath
  -> ('a * string, 'a * string) t

For a pair of (injectable) metadata and file content, it returns the unchanged metadata and the modified file content (injected into the template). As for reading metadata, an arrow can be described in the package of a template engine, for example Mustache, to reduce the number of modules to provide (we suppose that Renderable is defined in Yocaml_mustache and contains the Yaml_descriptor we defined earlier and the function to_string, of course):

let apply_as_template
    (type a) (module I : Yocaml.INJECTABLE with type t = a) template
  = Yocaml.apply_as_template (module I) (module Renderable) template

That's it! We can now propose a task that creates articles by correctly extracting the metadata and correctly injecting it into a template!

module Metadata = Yocaml_yaml
module Template = Yocaml_mustache

let create_article file =
  let target = Filename.concat "articles" (change_extension file "html") in
  create_file target (
    Metadata.read_file_with_metadata (module Article) file
    >>> snd Markdown.to_html
    >>> Template.apply_as_template (module Article) "templates/article.html"
    >>^ Stdlib.snd
  )

The symmetry between reading data and injecting it into a template is fun, and now we have a generic approach to building static, relatively configurable page generators. We can finally conclude!

The belated conclusion

In this article, we have briefly seen some of the details of how an aspiring Java Champion uses a library to generate, unproductively, his blog, through three axes:

There are still several aspects that I haven't covered (so as not to make this article too long), such as how to deal with dynamic dependencies, but perhaps that will be the subject of a future article. To conclude, Preface is pretty cool to use and you can try your hand at using YOCaml (if you like OCaml). There are several examples that can be used as a reference:

In addition, YOCaml has several plugins. In particular, one that allows you to directly generate pages in an Irmin storage, which can therefore be served by a MirageOS unikernel.

It was quite different from the previous articles because it was:

I hope you found it interesting to read and I'll see you soon for new articles!